若是一般化,仅仅两条角分线极端,会奈何样呢,底下就求解一下一般情形。
如下图,△ABC中,角A与角B外角中分线极端,即AD=BE。
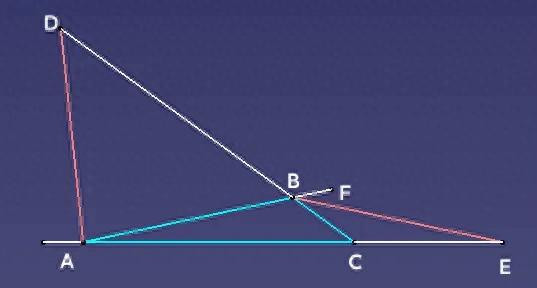
字据正弦定理BE/AB=sinA/sinE,
营区的杨树抽出了嫩芽,晨跑时能闻到泥土的清香。我刚当上排长没多久,浑身都是使不完的劲儿,整天琢磨着怎么带好这个排。
AD/AB=sin(180°-B)/sinD,由AD=BE可得sinA/sinE=sinB/sinD,化简得:
sinAsinD=sinBsinE。
又因为∠D=∠B-∠BAD=∠B-(90°-∠A/2)=(∠A/2+∠B)-90°,且∠E=∠FBE-∠A=(90°-∠B/2)-∠A=90°-(∠A+∠B/2)
代入sinAsinD=sinBsinE得:
-sinAcos(A/2+B)=sinBcos(A+B/2),积化和差后得:
-sin(A/2-B)-sin(3A/2+B)
=sin(A+3B/2)+sin(B/2-A),移项化简得sin(B-A/2)+(A-B/2)
=sin(3B/2+A)+sin(3A/2+B)。和差化积后得sin(A/4+B/4)cos(3B/4-3A/4)
=sin(5A/4+5B/4)cos(B-A)。
令A/4+B/4=α,B/4-A/4=β,代入上式可得sinαcos(3β)=sin(5α)cosβ,因为0<A<C<B<180°,且A+B<180°,彩娱乐专线是以sinα≠0,且cosβ≠0。
字据3倍角公式cos(3β)=4cos^3β-3cosβ是以4cos²β-3=sin(5α)/sinα,又2cos²β=1+cos(2β),代入上式化简得:2cos(2β)=sin(5α)/sinα+1。
将上式右边通分后和差化积,得
2cos(2β)=2sin(3α)cos(2α)/sinα,字据3倍角公式sin(3α)=-4sin^3α+3sinα,代入上式可得cos(2β)=(3-4sin²α)cos(2α)=(3-2(1-cos(2α)))cos(2α)=cos(2α)+cos²(2α)
=cos(2α)+1+cos(4α)。
令θ=2α,由于A<C<B,是以B>60°,是以0<2β<θ<90°,且θ=2α=A/2+B/2
=90°-C/2>90°-B/2>90°-60°/2=60°,是以2β=arccos(1+cosθ+cos(2θ)),60°<θ<90°。
是以A=θ-arccos(1+cosθ+cos(2θ))
B=θ+arccos(1+cosθ+cos(2θ))
C=180°-2θ
其中,θ是任一自在60°到90°之间的角,当θ=72°时,就获取文中着手的度数A=12°,B=132°,C=36°。因此彩娱乐,自在要求的三角形有大批个。

